جورج كانتور

التركيز الرئيسي لهذه الورقة هو وصف تطور جورج كانتور كعالم رياضيات وتسليط الضوء على رؤيته العميقة في هذا المجال. ولد كانتور في 3 مارس 1845 في سانت بطرسبرغ، روسيا، ويمكن القول إن أساس هذا الرياضي العظيم كان مبهراً بقدر ما كانت الرياضيات التي أنشأها لاحقاً. كانت طلاقته الرياضية الواسعة واضحة منذ البداية وقادته خلال مسارات جامعة برلين وجامعة غوتنغن.

في الأساس، كان العمل الهام لكانتور في مجال نظرية المجموعات، حيث سمى كثافة استثنائية تُعرف بالأعداد غير المنتهية. ذهب إلى أعماق الأعداد غير المنتهية ليخبرنا عن أحجام وخصائص المجموعات. وضع كانتور الأساس لهياكل غنية منها أصبح من الممكن فهم غموض اللانهائي عندما عرّف "المجموعة" على أنها مجموعة من العناصر المتميزة. أثبت للجمهور المتعلم أن اللانهائيات ليست كلها متساوية في الحجم

وجدت مجموعة الأعداد الطبيعية أنها لا نهائية بشكل أكبر من مجموعة الأعداد الصحيحة الموجبة، وكل عضو من المجموعة الجديدة يتوافق بطريقة جميلة مع بعض الأعداد الطبيعية. ومع ذلك، كانت الأعداد الحقيقية التي كانت لها نظرة خاطفة على الإمداد الحقيقي من اللانهائية الأكثر إثارة للدهشة والتي كانت بالفعل أسوأ بكثير من الأعداد الطبيعية من حيث الكثافة الفائقة التي كانت شائعة بينها.

من بين تصريحات كانتور البارزة والغامضة كانت فرضية الاستمرارية التي كانت وصفاً للوسط بين مجموعة الأعداد الطبيعية ومجموعة الأعداد الحقيقية. وبالتالي لا يزال العلم يجد نفسه في الظلام بشأن الإجابة على هذا السؤال، في سياقات نظرية المجموعات التقليدية؛ ومع ذلك، فإن هذه الفرضية نفسها اقترحت نوعاً من الاستقلالية.

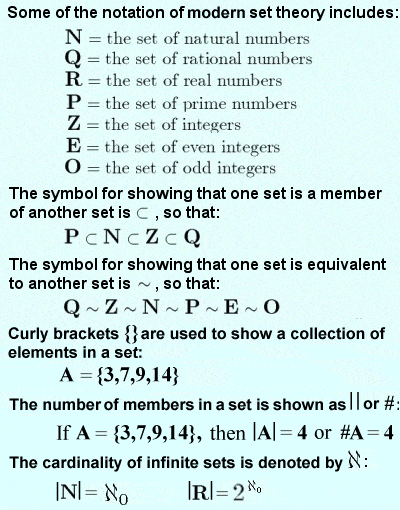
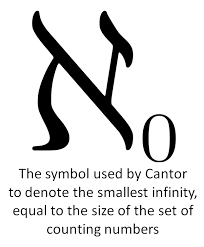
بعد التدقيق الدقيق والرفض، بدأت مساهمات كانتور تتلقى الثناء العام. تشمل انتصاراته من إنجازاته الأكاديمية حصوله على الأستاذية في جامعة هاله والاعتراف من المجتمعات العليا. ومع ذلك، كانت حياته الشخصية على الجانب الآخر من هذا النجاح وشملت الاكتئاب ومشاكل عقلية أخرى رغم الانتقادات.

إرث جورج كانتور في الرياضيات هو شهادة على استكشافه الجريء للانهائي. غيّر عمله إلى الأبد فهمنا للكون الرياضي، ملهمًا أجيالًا من المفكرين للشروع في رحلاتهم الخاصة عبر مناظر المعرفة اللامحدودة. يواصل روح كانتور في البحث عن المعرفة تردد صداها، كمنارة لأولئك الذين يجرؤون على التنقل في اللانهائي.